数学は正しいステップで学べば、誰でも『わかる!』 『できる!』ようになる科目です。

この記事が、皆さんの数学学習の悩みを解決し、自信を持って問題に取り組めるようになるための一助となれば幸いです。
数学の授業、なんだか呪文みたいでついていけない…
計算ミスが多くて、テストでいつも悔しい思いをしてる…
文章題になると、どこから手をつけていいか分からない…
もし、あなたがこんな風に感じているなら、心配いりません。多くの中学生が、数学に対して同じような悩みや苦手意識を持っています。
数学は、一つ一つの知識やスキルを積み重ねていく「積み上げ教科」。だからこそ、小学校の算数や中学1年生の最初でつまずいてしまうと、後からどんどん難しく感じてしまうことがあります。でも、それは決してあなたのせいではありません。
この記事では、数学が苦手だと感じている中学生に向けて、「わからない」をゼロにし、テストで着実に点数をアップさせるための具体的な勉強法を、基礎固めからテスト対策、モチベーション維持のコツまで、ステップバイステップで徹底解説します。
この記事を読めば、
- なぜ数学が難しく感じるのか、その理由がわかる
- 自分の「わからない」箇所を正確に見つけ、克服する方法がわかる
- 計算ミスや文章題など、よくあるつまずきポイントへの対策がわかる
- 定期テストや高校受験で結果を出すための戦略がわかる
- 忙しくても続けられる、やる気アップのヒントが見つかる
元数学教員の視点から、すぐに実践できる具体的なアドバイスをこれでもかと詰め込みました。
もう「数学キライ…」なんて言わせません!
一緒に、数学を得意科目に変えていきましょう。
なぜ数学は難しく感じるのか
ポイント: 数学は前の内容がわからないと次に進めない「積み上げ教科」。小学校の算数から抽象度が上がり、計算・文章題・図形などつまずきポイントも多い。でも、苦手なのはあなただけじゃない!
数学の勉強を始めようとしても、「何だかやる気が出ない」「どうせやっても分からない」と感じてしまうことはありませんか? まずは、多くの中学生がなぜ数学に苦手意識を持ってしまうのか、その理由を知ることから始めましょう。
原因がわかれば、対策も見えてきます。
「積み上げ教科」である理由
数学が他の科目と大きく違う点は、知識やスキルが階段のように積み重なっていく「積み上げ教科」であることです。
例えば、小学校で習う「分数・小数の計算」がしっかりできていないと、中学で習う「方程式」を解くのに苦労します。方程式が理解できていないと、「一次関数」や「連立方程式」に進むのが難しくなります。さらに、これらの内容が土台となって、高校数学へと続いていきます。
前の単元の理解が曖昧なまま次の単元に進んでしまうと、まるでグラグラの土台の上に家を建てるようなもの。 ちょっとした応用問題が出ただけで、途端にわからなくなってしまうのです。これが、数学で一度つまずくと、後から挽回するのが大変だと感じてしまう大きな理由です。

だからこそ、もし「わからない」と感じたら、勇気を持って前の単元に戻って復習することが、実は一番の近道になることも多いのです。
中学数学でつまずく典型 5 シーン
中学校の数学では、小学校の算数と比べて内容がより複雑になり、抽象的な考え方も求められるようになります。多くの中学生が、特に以下のような場面で「壁」を感じやすいようです。
| つまずきシーン | 具体的な悩み |
|---|---|
| ① 計算ミス連発 | 符号ミス(+と-)、分数・小数の計算間違い、移項ミス、単純な書き写し間違いが多い |
| ② 文章題アレルギー | 問題文が長いと読む気が失せる、何を問われているのか理解できない、式を立てられない |
| ③ 関数・グラフが謎 | y=ax+bと言われてもピンとこない、グラフの傾きや切片の意味がわからない、グラフを描けない |
| ④ 図形問題が苦痛 | 補助線がひらめかない、図形の性質や定理が覚えられない、証明問題が書けない |
| ⑤ 公式が覚えられない | たくさんありすぎて覚えきれない、丸暗記してもテストで使えない |
これらの「つまずき」は、決して特別なことではありません。多くの中学生が経験することです。大切なのは、「自分は数学が苦手なんだ…」と諦めてしまうのではなく、「どこで、どのようにつまずいているのか」を正確に把握し、一つ一つ解決していくことです。
その具体的な方法を見ていきましょう。
成績アップの土台づくり
ポイント: 成績アップの鍵は「基礎固め」。まず自分の弱点を知り、公式は意味から理解、ノートで思考を見える化し、「完全に解ける」まで反復練習しよう!
数学の成績を安定して伸ばしていくためには、しっかりとした「土台」を作ることが何よりも重要です。焦って応用問題に手を出す前に、まずは基本的な知識やスキルを確実に身につけることから始めましょう。
“わからない箇所”診断チェックリスト
「どこから手をつければいいかわからない…」という人は、まず自分の「わからない箇所」を正確に特定することからスタートしましょう。意外と、自分では気づいていない基礎的な部分でつまずいているケースは多いものです。
「自分の弱点はどこだろう?」を客観的に知るために、簡単な診断チェックリストを用意しました。 小学校の算数から中学数学の基本的な内容まで、理解度をセルフチェックできます。
このチェックリストを使うことで、
- どの単元の理解が曖昧なのか
- どの計算スキルが不足しているのか
- どこに戻って復習すべきか
が一目でわかります。自分の現在地を知ることが、効率的な学習の第一歩です。
中学生のための数学基礎力診断チェックリスト
はじめに このチェックリストで、数学の成績アップに欠かせない「基礎」がしっかり身についているか確認してみよう! 焦らず、正直に答えてね。「いいえ」や「少し不安」があっても大丈夫。自分の弱点を知ることが、得意になるための第一歩だよ!
使い方 以下の各項目について、今の自分に一番近いと思うものにチェック(✓)を入れてください。
【計算 分野】
- 小数の計算: 小数のたし算・ひき算・かけ算・わり算を、筆算を使って正確にできる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 分数のたし算・ひき算: 通分が必要な分数のたし算・ひき算を、正しく計算できる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 分数のかけ算・わり算: 約分を忘れずに、分数のかけ算・わり算を正しく計算できる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 計算の順序: かっこ( )や累乗(x2など)、かけ算・わり算、たし算・ひき算が混ざった計算を、正しい順序で計算できる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 正負の数の加減: 「−3+5」や「2−(−4)」のような、プラス・マイナスの数のたし算・ひき算が自信を持ってできる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 正負の数の乗除: 「(−3)×(−2)」や「10÷(−5)」のような、プラス・マイナスの数のかけ算・わり算の符号のルールを理解して計算できる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 文字式のルール: 「a×b=ab」や「1×x=x」のように、文字式の表し方のルールを理解している。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 同類項: 「3a+2b−a+5b」のような式で、同じ文字の項(同類項)を正しくまとめて簡単にできる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 分配法則: 「3(x+5)」や「−(a−b)」のような式で、かっこを正しく外すことができる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 一次方程式: 「2x−3=7」のような簡単な一次方程式を、移項を使って解くことができる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
【文章題・数量関係 分野】
- 割合: 「〇〇円の△△%はいくら?」や「□□円は△△円の何%?」といった割合の基本的な計算ができる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 速さ・時間・道のり: 「速さ=道のり÷時間」などの関係を使って、簡単な問題を解くことができる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 簡単な立式: 簡単な文章題を読んで、「何を x とおくか」を決め、自分で等式(方程式)を作ることができる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
【関数 分野】
- 比例・反比例: 比例 (y=ax) や反比例 (y=xa) の式やグラフの特徴を説明できる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 座標: 座標平面上で、点 (2,−3) のような座標の位置を正しく示すことができる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
【図形 分野】
- 基本図形の面積: 三角形、平行四辺形、台形、円の面積を求める公式を覚えている。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 基本立体の体積: 直方体、立方体、円柱、角柱の体積を求める公式を覚えている。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 平行線と角: 平行な直線に別の直線が交わるときにできる、同位角や錯角が等しいことを知っていて、角度の問題に使える。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 三角形の角: 三角形の内角の和が180°であることや、多角形の外角の和が360°であることを知っている。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
- 図形の用語: 「合同」「相似」「垂直」「平行」「円周率」などの基本的な図形の用語の意味を説明できる。
- [ ] はい
- [ ] 少し不安
- [ ] いいえ
結果の見方・次のステップ
お疲れ様でした! チェックは終わったかな?
- 「はい」が多かった人: 素晴らしい!基礎はしっかり身についている可能性が高いです。自信を持って、次のステップに進みましょう!
- 「少し不安」や「いいえ」があった人: 全然大丈夫!それがあなたの「伸びしろ」ポイントです。チェックがついた項目が、今復習すべき大切な基礎の部分です。
「いいえ」「少し不安」の項目が多かった分野については、焦らずに、もう一度教科書を読み返したり、小学校の内容に戻ってドリルを解いたりしてみましょう。 この記事の各セクションにも、克服するためのヒントがたくさん載っています。
自分の弱点を知ることが、数学を得意にするための大切なスタートです!
【注記】
- このチェックリストは、あくまで自己診断のための目安です。
- より正確な学力診断のためには、学校の先生に相談したり、テストの結果を分析したりすることも有効です。
チェックリストで「×」がついた箇所や、自信を持って「◎」をつけられなかった箇所が、あなたが重点的に復習すべきポイントです。必要であれば、小学校の教科書やドリルに戻ることを恐れないでください。
公式は「意味→使い方→暗記」の三段階で覚える
数学にはたくさんの公式が登場します。「全部丸暗記しなきゃ…」と思うと、気が重くなりますよね。しかし、公式はただ闇雲に暗記するのではなく、正しいステップで理解していくことが大切です。
おすすめは、以下の「意味→使い方→暗記」の三段階で覚える方法です。
- 【意味】 なぜ、この公式が成り立つのか?
- 教科書の説明をじっくり読んだり、先生に質問したりして、公式が導き出される背景や理屈を理解しようと努めましょう。「なぜそうなるの?」という疑問を持つことが大切です。
- 例えば、三角形の面積が「底辺×高さ÷2」になる理由を、長方形の面積との関連で説明できますか?
- 【使い方】 どんな問題で、どうやって使うのか?
- 公式の意味が理解できたら、次は具体的な問題を通して使い方をマスターします。教科書の例題や基本的な練習問題を解いてみましょう。
- 「この問題では、どの公式を使えばいいんだろう?」「公式の文字に、問題文のどの数字を当てはめればいいんだろう?」と考えながら解くことが重要です。
- 【暗記】 スラスラ言える&書けるようにする
- 意味と使い方を理解した上で、最終段階として公式そのものを正確に覚えます。何度も声に出して読んだり、ノートに書いたりして、何も見なくても思い出せるようにしましょう。
- 公式を覚えるためのカードを作ったり、アプリを活用したりするのも効果的です。
丸暗記だけに頼ると、少し問題の形が変わっただけで手も足も出なくなってしまいます。「意味」と「使い方」をしっかり理解することで、公式は初めて「使える武器」になるのです。
思考を可視化するノート術
数学のノートは、ただ先生の板書を書き写すだけではもったいない! ノートは、あなたの「考え方」を整理し、間違いを発見し、復習を効率化するための最強ツールになります。

<成績が上がるノート術 5つのポイント>
- 日付と単元名を必ず書く: いつ、何を学習したのかを明確にし、後で見返しやすくします。
- 途中式は省略せず、必ず書く: これが最重要!計算ミスを見つけやすくなるだけでなく、自分がどう考えて問題を解いたのか、そのプロセスを後から確認できます。間違いの原因究明に役立ちます。
- 図やグラフは大きく、丁寧に描く: 特に図形問題や関数問題では、フリーハンドでも良いので、定規なども使いながら、問題の状況が把握しやすいように大きく書きましょう。分かったこと(長さ、角度、座標など)はどんどん書き込みます。
- 色ペンはルールを決めて使う: 重要だと思う公式や定理、間違えた箇所、先生が強調したポイントなど、自分なりのルールを決めて色分けすると、復習の効率が格段にアップします。(例:赤=重要公式、青=間違えた箇所、緑=先生のコメント)
- 余白を意識する: ノートいっぱいにギチギチに書くのではなく、適度な余白(スペース)を空けておきましょう。後から気づいたことや、復習時のメモ、関連する問題を書き加えるのに役立ちます。吹き出しを使って、自分の言葉でポイントや注意点をメモするのもおすすめです。
「ノートは思考を整理するための場所」と考え、後から見返したときに、授業内容や自分の考えがしっかり再現できるようなノート作りを目指しましょう。
完全に「解ける」までの反復練習プロトコル
数学の力を伸ばすには、スポーツや楽器の練習と同じように、正しい方法で、十分な量の反復練習が欠かせません。ただ問題を解くだけでなく、「完全に解ける」ようになるまで繰り返すことが重要です。
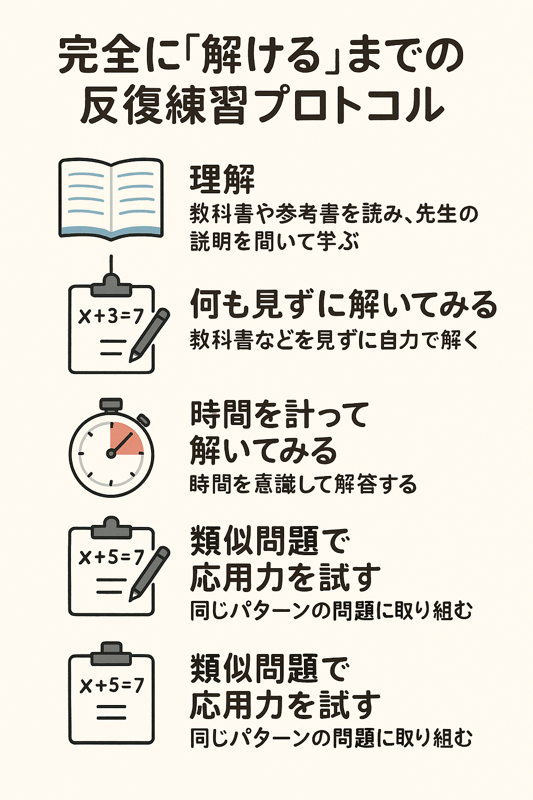
<「解ける」レベルになるための反復練習プロトコル>
- まずは「理解」する: 教科書や参考書を読み、先生の説明を聞いて、問題の解き方や関連する公式・定理の意味をしっかり理解します。わからない点はそのままにせず、質問して解決しましょう。
- 「真似て」解いてみる: 理解できたら、例題などを見ながら、まずは解き方を真似て自分で解いてみます。途中式も丁寧に書きましょう。
- 「何も見ずに」解いてみる: 解き方の手順を覚えたら、今度は教科書や解答を見ずに、自力で解けるか挑戦します。ここでスラスラ解ければOK。もし詰まったり、間違えたりしたら、ステップ1や2に戻って確認します。
- 「時間を計って」解いてみる: 自力で正確に解けるようになったら、次は時間を意識して解いてみましょう。テスト本番を想定し、スピードも高めていきます。
- 「類似問題」で応用力を試す: 同じパターンの、少し数字や設定が違う問題を解いて、応用力が身についているかを確認します。
- 「忘れた頃に」もう一度解く: 一度完璧に解けるようになっても、人間は忘れてしまう生き物です。1週間後、1ヶ月後など、時間を空けてもう一度解き直し、知識が定着しているかを確認しましょう。
練習問題を解く際には、「◎○△×」システムを活用するのがおすすめです。
- ◎: 自信を持って、完璧に解けた!
- ○: 解けたけど、ちょっと自信がない or 少し時間がかかった
- △: 途中まで分かったけど、最後で詰まった or ヒントが必要だった
- ×: 全く分からなかった or 間違えた
復習する際は、「×」や「△」の問題を中心に、最終的に全ての問題が「◎」になるまで繰り返しましょう。 この地道な繰り返しが、確かな実力へと繋がります。
つまずきタイプ別★即効処方せん
ポイント: 計算ミス、文章題、関数、図形…それぞれの苦手には原因と対策がある!自分のタイプに合わせて、具体的な解決策を試してみよう。
数学の苦手なポイントは人それぞれ。ここでは、中学生が特につまずきやすい4つのタイプ別に、すぐに試せる具体的な解決策(処方せん)を紹介します。自分がどのタイプに当てはまるかチェックして、対応する項目を読んでみてください。
| タイプ | 代表的な症状 | 処方せん(クリックして詳細へ) |
|---|---|---|
| 計算ミス多発 | 符号/写し間違いが多い | 「うっかりミス」撲滅 3 ステップ |
| 文章題アレルギー | 問題文を読むだけでパニックになる | 文章題を分解→図解→数式化する手順 |
| 関数が謎 | y=ax+b がピンとこない | 関数とグラフを結ぶ“往復練習”法 |
| 図形・証明が苦痛 | 補助線が浮かばない、証明が苦手 | 図形証明をロジックツリーで書くコツ |
「うっかりミス」撲滅 3 ステップ
「わかっていたはずなのに、また計算ミスしちゃった…」そんな悔しい経験はありませんか? ケアレスミスは、ちょっとした意識と工夫で確実に減らせます。
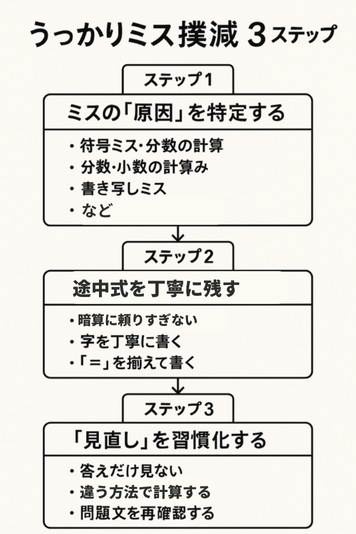
<ステップ1: ミスの「原因」を特定する> まずは、自分がどんなミスをしやすいのか、そのパターンを知ることが大切です。テストや問題集の間違いを見直し、ミスの種類を分類してみましょう。
- 符号ミス(+と-の付け忘れ、外し忘れ)
- 分数・小数の計算ミス(通分、約分、小数点の位置)
- 移項ミス(=をまたぐときの符号変化)
- 書き写しミス(問題文や途中の数字を写し間違える)
- 単純な計算間違い(九九レベル、足し算引き算)
- 問題文の読み間違い・条件の見落とし
自分のミスの傾向がわかれば、対策も立てやすくなります。
<ステップ2: 「途中式」を丁寧に残す> 面倒くさがらずに、計算の過程を一つ一つ丁寧に書く習慣をつけましょう。
- 暗算に頼りすぎない: 特に複雑な計算や符号が絡む場合は、必ず書き出す。
- 字を丁寧に書く: 自分で書いた数字や記号が読めなくてミスすることも。「6」と「0」、「1」と「7」など、紛らわしい字は特に注意。
- 「=」を揃えて書く: 式が縦に揃っていると、見直しやすくなります。
途中式は、間違いを発見するための「証拠」になります。どこで間違えたのかが一目でわかるので、効率的な復習にも繋がります。
<ステップ3: 「見直し」を習慣化する> 問題を解き終わったら、必ず見直し(検算)をする習慣をつけましょう。
- 答えだけ見ない: 答えだけでなく、計算過程(途中式)も一つ一つチェックする。
- 違う方法で計算してみる: 可能であれば、別の計算方法で確かめてみる(例:足し算の検算は引き算で)。
- 問題文を再確認する: 問いに正しく答えているか、条件を見落としていないか、もう一度問題文を読む。
- テストでは見直し時間を確保する: 問題を解き終える時間だけでなく、必ず5分~10分程度の見直し時間を確保できるように、時間配分を意識しましょう。
「ミスはするもの」という前提で、それを発見し修正する仕組みを自分の中に作ることが大切です。
文章題を分解→図解→数式化する手順
文章題が苦手な人は、問題文のどこから手をつけていいか分からず、混乱してしまうことが多いようです。文章題を攻略する鍵は、情報を整理し、「見える化」することです。
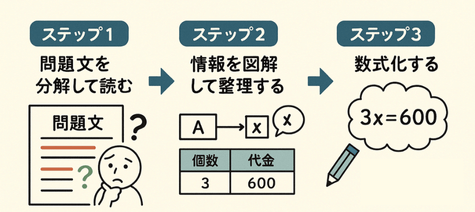
<ステップ1: 問題文を「分解」して読む> まずは焦らず、問題文を丁寧に読み解くことから始めます。
- 何がわかっているか(既知の情報)?: 問題文中の数字や条件に下線を引いたり、印をつけたりして整理します。「速さは?」「長さは?」「個数は?」など。
- 何を求められているか(未知の情報)?: 最終的に何を答えればよいのかを明確にします。問いの部分に印をつけましょう。
- わからない言葉はないか?: 意味がわからない言葉があれば、必ず確認します。
<ステップ2: 情報を「図解」して整理する> 文章だけではイメージしにくい関係性を、図や表、線分図、簡単なイラストなどを使って「見える化」します。
- 関係性を矢印などで示す: 「AはBより大きい」「〇〇と△△を合わせると…」といった関係を図で表します。
- 時間経過や物の動きを図にする: 「速さ・時間・道のり」の問題などは、線分図や簡単な図を描くと状況が把握しやすくなります。
- 情報を表にまとめる: 個数や代金、割合など、複数の要素が絡む場合は、表に整理すると分かりやすくなります。
<ステップ3: 図や整理した情報から「数式化」する> 図解して整理した情報をもとに、立式(方程式など)します。
- 求めたいものを文字(x など)で置く: 何を x と置くかを明確にします。
- 等しい関係を見つける: 問題文や図の中から、「〇〇 = △△」となる関係性を見つけ出し、それを数式で表現します。
- 単位を確認する: 長さ(cm, m, km)、時間(秒, 分, 時)など、単位が揃っているか確認しましょう。
文章題は、国語の読解力も重要になります。問題文を正確に読み取る練習も意識しましょう。最初は時間がかかっても、この「分解→図解→数式化」のステップを繰り返すうちに、スムーズに解けるようになっていきます。
関数とグラフを結ぶ“往復練習”法
「関数って何?」「グラフってどう描くの?」関数は中学数学の大きな山場の一つです。関数を理解するコツは、「式」と「グラフ」をセットで考え、行ったり来たりする練習をすることです。
<式の情報を「グラフ」に反映させる練習>
- 座標を理解する: x 座標と y 座標の意味、点のプロットの仕方を確実にマスターしましょう。
- 式から点をプロットする: 一次関数 y=ax+b なら、まずは切片(x=0 のときの y の値)の点を打ちます。次に、x=1,2,−1 などを代入して他の点の座標を求め、グラフ上に点を打ち、それらを結びます。
- 傾きと切片の意味をグラフで理解する:
- 切片 b: グラフが y 軸と交わる点の y 座標。
- 傾き a: x が 1 増えたときに y がどれだけ増える(減る)かを表す割合。グラフ上では「右に1進んだときに、上にいくつ進むか(下にいくつ進むか)」で確認できます。
- 二次関数 y=ax2: x にいくつか値を代入して (x,y) のペアを作り、点をプロットして滑らかな曲線(放物線)で結びます。a の値によってグラフの開き具合や向きがどう変わるかを確認しましょう。
<グラフの情報を「式」に反映させる練習>
- グラフから切片と傾きを読み取る: グラフが与えられたときに、y 軸との交点から切片 b を読み取ります。次に、グラフ上の分かりやすい2点を見つけ、x の増加量と y の増加量から傾き a を求めます。(傾き = y の増加量 / x の増加量)
- グラフが通る点の座標を式に代入する: グラフが特定の点 (p,q) を通ることがわかっている場合、その座標を関数の式(例: y=ax+b)に代入して、a や b に関する方程式を作ることができます。
- グラフの形から関数の種類を判断する: 直線なら一次関数、放物線なら二次関数、といったように、グラフの概形から関数の種類を推測します。
この「式→グラフ」「グラフ→式」の”往復練習”を繰り返すことで、両者の関係性が感覚的に理解できるようになります。関数問題では、わかった情報をどんどんグラフに書き込んでいくことも、問題を解く上で非常に有効なテクニックです。
図形証明をロジックツリーで書くコツ
「図形問題、どこから考えればいいかわからない…」「証明問題、何を書けばいいの?」図形や証明が苦手な人は、論理的に考えるプロセスに慣れていないことが多いです。ここでは、証明問題を「ロジックツリー」のように考えるコツを紹介します。
<ステップ1: 「ゴール(結論)」と「スタート(仮定)」を確認する>
- ゴール(結論): この証明で最終的に示したいことは何か?(例:「△ABC ≡ △DEF を示したい」「AB // CD を示したい」)
- スタート(仮定): 問題文で与えられている条件は何か?図に書かれている情報は何か?(例:「AB = DE」「∠BAC = ∠EDF」「四角形ABCDは平行四辺形」)
- 図に情報を書き込む: 仮定で与えられた辺の長さや角度、平行などの情報を、図の中に記号などを使って分かりやすく書き込みます。
<ステップ2: ゴールから逆算して「必要な要素」を考える> ゴール(結論)を示すためには、何が言えれば良いのかを逆算して考えます。
- 例:「△ABC ≡ △DEF」を示したい場合
- → そのためには、合同条件(3辺相等、2辺夾角相等、1辺両端角相等)のどれかが言えれば良い。
- → 例えば「2辺夾角相等」を使うなら、「AB=DE」「AC=DF」「∠BAC=∠EDF」の3つが言えれば良い。
<ステップ3: スタート(仮定)から「言えること」を繋げていく> スタート(仮定)の情報と、図形の基本的な性質や定義、定理を使って、ステップ2で考えた「必要な要素」を導き出せないか考えます。
- 例:「AB=DE」は仮定にあるか?なければ、他の条件から導けないか?
- 「∠BAC=∠EDF」は仮定にあるか?なければ、他の条件(例:平行線の錯角・同位角など)から導けないか?
- 「AC=DF」は仮定にあるか?なければ…?
この「ゴールから逆算」と「スタートから順算」を組み合わせ、結論に至るまでの論理的な道筋(=証明の根拠となるステップ)を繋げていくのが、証明問題の基本的な考え方です。
<ロジックツリー的に書き出す> 慣れないうちは、以下のように箇条書きで書き出してみると、思考が整理しやすくなります。
【結論】△ABC ≡ △DEF
↑ そのためには?(合同条件:例 2辺夾角相等)
├─ ① AB = DE (← これはどこから言える? 仮定 or 定理?)
├─ ② AC = DF (← これはどこから言える? 仮定 or 定理?)
└─ ③ ∠BAC = ∠EDF (← これはどこから言える? 仮定 or 定理?)
↑ これらの根拠は?
├─ 仮定より:…
├─ 平行線の錯角(同位角)より:…
├─ 〇〇の定義より:…
└─ 定理〇〇より:…
証明問題はパズルのようなものです。定義や定理というルールを使って、仮定というピースから結論という完成形を組み立てる練習を繰り返しましょう。補助線は、この道筋を見つけるためのヒントになることがあります。基本的な補助線の引き方も練習しておくと良いでしょう。
テストで結果を出す戦略
ポイント: テスト成功の鍵は準備と戦略!教科書・ワークを完璧にし、計画的に勉強を進め、本番での時間配分とテスト後の復習をマスターしよう。
日々の学習の成果をテスト本番でしっかり発揮するためには、戦略的な準備が欠かせません。ここでは、定期テストやその先の高校受験で確実に結果を出すための方法を紹介します。
教科書&ワークを“100%活かす”チェックリスト
テスト勉強というと、難しい問題集に手を出すべきか悩む人もいますが、最も重要な教材は、実は普段使っている「教科書」と「学校のワーク」です。なぜなら、テスト問題の多くは、これらをベースに作られているからです。
<教科書&ワーク 徹底活用チェックリスト>
- [ ] 教科書の例題・練習問題は、何も見ずに解けるか?
- 解けない問題は、解説を読んで理解し、必ず自力で解けるようになるまで繰り返す。
- [ ] 教科書の重要語句・定義・公式は、自分の言葉で説明できるか?
- ただ覚えるだけでなく、意味を理解しているか確認する。
- [ ] 学校のワーク(問題集)は、最低1周は解き終えたか?
- テスト範囲の問題は、全て一度は解いておく。
- [ ] ワークで間違えた問題(×や△)に印がついているか?
- 弱点を明確にし、繰り返し解き直すために必須。
- [ ] 間違えた問題は、解答解説を読んで理解したか?
- なぜ間違えたのか、正しい解き方は何かを必ず確認する。
- [ ] 間違えた問題は、時間を置いてから再度解き直し、自力で解けるようになったか?
- 「わかったつもり」で終わらせず、「できる」状態にする。
- [ ] ワークを2周目、3周目と繰り返しているか?(特に苦手な単元や間違えた問題)
- 目標は、ワークの問題をほぼ100%(少なくとも90%以上)自力で解ける状態にすること。
- [ ] 先生が授業中に「重要だ」と言っていた箇所は、特に重点的に復習したか?
- テストに出やすいポイントである可能性が高い。
市販の難しい問題集に手を出すのは、教科書と学校ワークの内容を完璧にしてからでも遅くありません。まずは、この最も基本的な教材を徹底的に使い倒しましょう。
テスト 2 週間前からの逆算スケジュール表
テスト直前に慌てて勉強を始めても、十分な対策はできません。特に数学のように積み重ねが重要な科目は、計画的な学習が不可欠です。テスト2週間前(遅くとも1週間前)からは、テストモードに切り替え、逆算してスケジュールを立てましょう。
<逆算スケジュールの立て方(例)>
- ゴール(テスト当日)を設定: テストの日時と科目を確認します。
- テスト範囲を確認: 各科目の正確なテスト範囲を把握します。(数学なら「〇〇ページから△△ページまで」「単元名」など)
- やるべきことをリストアップ: 数学のテスト範囲について、やるべきこと(ワークの解き直し、教科書の復習、苦手な単元の練習など)を具体的に書き出します。
- 日ごとのタスクに分解: リストアップした「やるべきこと」を、テストまでの日数で割り振り、1日あたりに取り組む内容と量の目安を決めます。「この日はワークのP.〇〇~△△を解き直す」「この日は関数の復習に1時間使う」など。
- 予備日を設ける: 計画通りに進まないこともあるので、調整用の予備日を1~2日設けておくと安心です。
- 他の科目とのバランスも考慮: 数学だけでなく、他の科目の勉強時間も考慮して、無理のない計画を立てましょう。
(ここに簡単なスケジュール表のテンプレート例を挿入するイメージ)
| 日付 | 曜日 | やること(数学) | 他教科 | 達成度 |
| 〇/〇 (2週間前) | 月 | テスト範囲確認、ワークP.10-15解き直し(基本問題) | 英語 単語 | 〇〇% |
| 〇/〇 | 火 | 教科書 例題復習(〇〇単元)、ワークP.16-20解き直し | 理科 ノート | 〇〇% |
| … | … | … | … | … |
| 〇/〇 (前日) | 日 | 全範囲の最終チェック、間違えた問題の見直し | 全教科 暗記 | 〇〇% |
| 〇/〇 (当日) | 月 | テスト本番! |
計画を立てることで、「何を」「いつまでに」「どれくらい」やればいいのかが明確になり、安心して勉強に取り組めます。計画通りに進んだら、自分を褒めてあげることも忘れずに!
本番で点を落とさない時間配分術
せっかく勉強したのに、「時間が足りなくて最後まで解けなかった…」というのは、非常にもったいないですよね。テスト本番で実力を最大限に発揮するためには、時間配分を意識することが重要です。
<テスト本番の時間配分 3つのコツ>
- 「始め!」の合図で、まず全体を見渡す(1分程度):
- 問題の構成(大問の数、小問の数、配点)をざっと確認します。
- どの問題にどれくらいの時間をかけられそうか、大まかな見当をつけます。
- パッと見て「解けそう!」と思える問題や、配点の高い問題に目星をつけておくのも良いでしょう。
- 解ける問題から確実に解く:
- 難しい問題で悩み込んで時間を浪費するのは避けましょう。まずは、自分が確実に解ける問題から手をつけて、得点を積み重ねていきます。
- 少し考えて「これは時間がかかりそうだ」「難しそうだ」と感じたら、一旦その問題は飛ばして、後で時間があれば戻ってくる勇気も大切です。印をつけておくと良いでしょう。
- 大問ごと、または問題ごとに時間制限を意識する:
- テスト全体の時間と問題数から、1問あたりにかけられる平均時間を計算しておき、それを目安にします。(例:50分で大問5つなら、1つの大問あたり10分弱)
- 時計を意識し、「この問題はあと〇分で切り上げよう」といった判断ができるように練習しておきましょう。過去問や模試で時間を計って解く練習が効果的です。
そして最も重要なのが、「見直し時間」を必ず確保すること。 理想はテスト終了時間の5~10分前には一通り解き終わり、残りの時間で見直し(計算ミスチェック、問題文の読み間違いチェック、解答欄のズレチェックなど)に充てられるようにペース配分を考えましょう。
テスト後 24h 以内にすべき復習メソッド
テストが終わるとホッとして、結果が返ってくるまで何もしたくなくなるかもしれません。しかし、テストは受けっぱなしでは意味がありません。 記憶が新しいうちに復習することで、学びの効果は格段に高まります。
<テスト後24時間以内に行いたい「即効復習」>
- 自己採点(可能であれば): 問題用紙に自分の解答をメモしておき、テスト後にすぐ自己採点してみましょう。どの問題ができて、どの問題ができなかったのかを把握します。
- 「できなかった問題」を再現してみる: 解けなかった問題や、自信がなかった問題について、「どう考えたか」「どこで詰まったか」を思い出せる範囲でノートに書き出してみます。
- 正しい解き方を確認する: 友達と答え合わせをしたり、先生に質問に行ったり、解説が配られたらそれを読んだりして、正しい解き方を確認します。
- 「なぜ間違えたか」を分析する:
- 単なる計算ミス? → 計算ミス対策を強化
- 公式や定理を覚えていなかった? → 基礎知識の定着を強化
- 問題の意味を取り違えていた? → 読解力、問題文の読み方を改善
- 時間が足りなかった? → 時間配分の練習、解くスピード向上
- 応用力が足りなかった? → 基礎固めの上で、応用問題の練習
- 解き直しをする: 間違えた問題は、必ず自分の力で解けるようになるまで、解説を見ながらでも良いので解き直します。
テストは、自分の理解度や弱点を客観的に知るための絶好の機会です。 結果の点数に一喜一憂するだけでなく、テストを「学びを深めるためのツール」として最大限に活用しましょう。この「即効復習」を習慣にすることで、次のテスト、そしてその先の高校受験に向けて着実に力をつけていくことができます。
忙しくても続く!モチベーション維持術
ポイント: やる気が出ない時もあるけど大丈夫!小さな成功体験を大切にし、スキマ時間を活用、困ったら質問する勇気を持とう。
「数学の勉強、やらなきゃいけないのは分かってるけど、なかなかやる気が出ない…」「部活や他の勉強で忙しくて、時間が取れない…」そんな悩みを持つ中学生も多いはず。ここでは、忙しい毎日の中でも数学学習を続け、モチベーションを保つためのヒントを紹介します。
「小さなできた!」を見える化する◎○△ノート
なかなか成果が見えにくいと、勉強を続けるのが辛くなってしまいますよね。だからこそ、日々の「小さな進歩」や「できた!」という感覚を大切にすることが重要です。
そこでおすすめなのが、先ほども紹介した「◎○△×ノート(システム)」の活用です。
- 練習問題を解くたびに、自信度に応じて印をつける。
- 最初は「×」や「△」が多かった問題が、繰り返し解くうちに「○」になり、最終的に「◎」に変わっていく過程を「見える化」する。
<「できた!」を増やすコツ>
- 簡単な問題から始める: いきなり難しい問題に挑戦するのではなく、まずは自分が確実に「◎」をつけられるレベルの問題から始め、成功体験を積み重ねましょう。
- 目標を小さく設定する: 「今日はワークを1ページだけ完璧にする」「計算問題を5問だけ解く」など、達成しやすい小さな目標を設定し、クリアできたら自分を褒めてあげましょう。
- 進捗を記録する: ノートだけでなく、カレンダーや手帳に「今日は〇問解けた!」「苦手な単元を復習した!」など、頑張ったことを記録していくのも効果的です。
目に見える形で自分の成長を確認できると、「もう少し頑張ってみようかな」という気持ちが自然と湧いてきます。
スキマ 10 分で知識を固めるカード学習
「まとまった勉強時間が取れない…」という人におすすめなのが、「スキマ時間」の活用です。10分程度の短い時間でも、工夫次第で効果的な学習ができます。
<スキマ時間活用アイデア>
- 公式・定理暗記カード: 覚えたい公式や定理、重要な用語などを書いたカード(単語帳や自作カード、スマホアプリでもOK)を作り、通学中の電車やバスの中、休み時間、寝る前などの短い時間で見直します。
- 1問集中ドリル: 計算問題や基本的な問題を1〜2問だけ、タイマーで10分計って集中して解いてみる。
- 前回の授業ノート見返し: 授業の前後5分で、前回のノートをサッと見返すだけでも、記憶の定着に繋がります。
- 解説動画視聴: オンライン学習サービスの短い解説動画(5〜10分程度)を、移動中などに視聴する。
ポイントは、「完璧にやろう」と思わないこと。 「10分だけでも、数学に触れる時間を作る」という意識で、気軽に、そして継続的に取り組むことが大切です。チリも積もれば山となる、です!
質問力を鍛える 3 つのフレームワーク
「わからないことがあっても、何て質問していいかわからない…」「先生に質問しに行くのが恥ずかしい…」そんな経験はありませんか? 質問することは、決して恥ずかしいことではなく、むしろ賢い学習戦略です。上手に質問できるようになると、学習効率は格段に上がります。
<上手な質問をするための3つの準備>
- 「どこまでわかって、どこからわからないのか」を明確にする:
- 質問する前に、問題のどこまでは自分で理解できたのか、どの部分で手が止まってしまったのかを具体的に説明できるように整理しておきましょう。
- (例:「この問題の、この式を立てるところまでは分かったのですが、次の計算がなぜこうなるのか分かりません」)
- 「自分で考えたこと・試したこと」を伝える:
- ただ「わかりません」と言うだけでなく、「自分はこう考えてみたのですが、ここが違うのでしょうか?」「この公式を使おうとしたのですが、上手くいきませんでした」のように、自分で試行錯誤した過程を伝えることで、先生もより的確なアドバイスをしやすくなります。
- 「具体的な質問」を用意する:
- 漠然とした質問ではなく、「〇〇の定義について、もう一度説明していただけませんか?」「この問題の別解はありますか?」のように、何を知りたいのかを具体的に聞きましょう。
<質問フレームワーク(例)> 「〇〇(単元名や問題番号)について質問があります。 (ステップ1)私は、□□の部分までは理解できた(または、こう考えた)のですが、 (ステップ2)△△の部分(または、ここから先)がわかりません。 (ステップ3)具体的には、××はなぜこうなるのでしょうか?(または、××について教えてください)」
最初は勇気がいるかもしれませんが、先生や友達、家族など、頼れる人に積極的に質問してみましょう。質問を通して理解が深まるだけでなく、コミュニケーション能力も鍛えられます。
保護者サポート Q&A
ポイント 保護者の方は、お子さんの「わからない」に寄り添い、結果だけでなくプロセスを褒め、適切な学習環境を整えるサポートを。
ここでは、保護者の皆様からよく寄せられる数学学習に関するご質問に、Q&A形式でお答えします。お子様の数学学習をサポートする上でのヒントとしてご活用ください。
- 子どもが「わからない」と言ったときの声かけは?
-
まず、「わからない」と言えたことを認めてあげてください。「質問してくれてありがとう」「どこがわからないか一緒に考えてみようか」と、お子様の気持ちに寄り添う姿勢が大切です。「なんでこんなことも分からないの!」といった否定的な言葉は、お子様の学習意欲を削いでしまう可能性があるので避けましょう。 具体的には、「どこまでは分かった?」「どの部分で困ってる?」と、つまずいている箇所を特定する手助けをしてあげると良いでしょう。すぐに答えを教えるのではなく、教科書やノートを見返すように促したり、ヒントを与えたりしながら、お子様自身が考えるプロセスをサポートする関わり方が理想的です。どうしても分からない場合は、「一緒に先生に聞きに行こうか?」と提案するのも良い方法です。
- 塾に行かない学習で気をつけることは?
-
塾に通わずに家庭学習を進める場合、「学習計画」「進捗管理」「質問できる環境」の3点が特に重要になります。
- 学習計画: 学校の進度に合わせて、無理のない学習計画を一緒に立ててあげましょう。この記事で紹介したような、教科書・ワーク中心の学習を基本とし、「いつ」「何を」「どれくらい」やるのかを明確にします。
- 進捗管理: 定期的に学習の進捗状況を確認し、計画通りに進んでいるか、困っていることはないかなどを話し合う機会を持ちましょう。ただし、管理しすぎるとお子様の自主性を損なう可能性もあるため、適度な距離感を保つことが大切です。
- 質問できる環境: 家庭内で解決できない疑問点が出てきた場合に、学校の先生や、場合によってはオンライン教材の質問サービスなどを活用できるよう、事前に相談しておくと良いでしょう。「わからないことを聞ける場所がある」という安心感は、学習を進める上で大きな支えになります。
- 親ができる進捗チェックのポイントは?
-
テストの点数という「結果」だけを見るのではなく、日々の学習の「プロセス」に注目してあげることが大切です。
- ノートを見る: 丁寧にノートを取っているか、途中式をしっかり書いているかなどをチェックします。「きれいに書けてるね」「図が分かりやすいね」といった具体的な声かけは、お子様のモチベーションに繋がります。
- 学習時間や課題の達成度を確認する: 「今日は計画通りに進んだ?」「どんなところが難しかった?」など、プレッシャーにならない程度に日々の取り組みについて聞いてみましょう。頑張りを具体的に褒めることが重要です。
- 「できた!」を共有する: お子様が「この問題、解けるようになった!」と報告してくれたら、一緒に喜び、その努力を認めましょう。「すごいね!頑張ったね!」という肯定的なフィードバックが、次への意欲を引き出します。
過度な干渉は避けつつも、お子様の学習状況に関心を持ち、努力を認め、困ったときには相談に乗るというスタンスで、温かく見守ってあげてください。
文章題が苦手な場合、数学的な思考力だけでなく、問題文を正確に読み取る国語力も影響していることがあります。国語の勉強法については、こちらの記事も参考にしてみてください。 → [ 中学生むけ:国語 勉強法 ]
最新の学習指導要領における数学の目標については、文部科学省のサイトで確認できます。 → [ 文部科学省 学習指導要領 ]
まとめ&今日から始める 3 アクション
ポイント: 数学は正しい方法で努力すれば必ず得意になる!まずは診断で弱点を知り、苦手なテーマを1つ解決し、テスト計画を立てることから始めよう!
今回は、中学生が数学の勉強でつまずきやすいポイントと、それを克服して成績を上げるための具体的な方法について解説してきました。
数学は「積み上げ教科」だからこそ、基礎をしっかり固めることが何よりも大切です。 そして、公式は丸暗記ではなく意味を理解し、ノートで思考を整理し、正しい方法で反復練習を重ねることが、着実な力に繋がります。計算ミスや文章題、関数、図形といった苦手分野も、原因を知り、適切な対策をとれば必ず克服できます。
テストで結果を出すためには、計画的な学習と時間配分、そして復習が鍵となります。そして何より、「小さなできた!」を大切にし、諦めずに学習を続けることが、モチベーションを保つ秘訣です。
結果が出るまでには時間と努力が必要ですが、この記事で紹介した方法を一つでも実践すれば、必ずあなたの数学力は向上します。自信を持ってください!
さあ、今日から行動を起こしましょう! まずは、以下の3つのアクションから始めてみませんか?
- 「わからない箇所診断」をチェックして基礎確認: まずは自分の現在地を知ることから。前のセクションで紹介した診断チェックリストを実施して、どこに弱点があるのかを確認しましょう。
- つまずきタイプ別の章を読んで1テーマだけ解決: 「つまずきタイプ別★即効処方せん」の中から、今の自分が一番悩んでいるテーマを一つ選び、その解決策を今日から試してみましょう。
- テストまでの逆算スケジュールを立てる: 次の定期テストに向けて、「テスト 2 週間前からの逆算スケジュール表」を参考に簡単な学習スケジュールを立ててみましょう。計画を立てるだけで、やるべきことが明確になります。
柔軟な学びを選びたいなら(ID学園紹介)
ポイント: もっと自分のペースで数学を学びたいなら、通信制+αのID学園も選択肢の一つ。オンラインサポートやID型AI学習(オプション)も充実。
ここまで、中学校の数学を克服するための様々な勉強法を紹介してきました。しかし、「決まった時間に授業を受けるのが苦手」「もっと自分のペースで、わからないところをじっくり教えてほしい」と感じている人もいるかもしれません。
もしあなたが、より柔軟で、自分に合った学び方を探しているなら、通信制高校という選択肢もあります。
ID学園は、オンライン+通学を中心とした通信制の仕組みと、一人ひとりに合わせた個別指導を組み合わせた、新しいタイプの学びの場です。
- 自分のペースで学習を進められる: 毎日通学する必要がなく、自分の理解度に合わせて学習計画を立て、得意な科目はどんどん先に、苦手な科目はじっくり時間をかけて取り組むことができます。
- 数学の個別サポートも充実: オンラインでの個別指導を通じて、わからない箇所をすぐに質問し、理解できるまで丁寧に教えてもらうことが可能です。周りを気にせず、自分の疑問解消に集中できます。
- AI学習など最新の学習ツールも活用: 一人ひとりの苦手分野をAIが分析し、最適な問題を出題してくれるAI学習(オプション)など、効率的に学力を伸ばすためのツールも用意されています。(※提供サービスは変更される場合があります)
「集団授業だとなかなかついていけない」「もっと自分の弱点に合わせた指導を受けたい」と感じているなら、ID学園のような学び方がフィットするかもしれません。
高校での学び方は一つではありません。自分らしいペースで、無理なく、そして着実に力を伸ばしていける環境を見つけることが大切です。









